卡诺图及其画法
发布时间:2013/10/18 20:27:57 访问次数:16470
为了便于化简,把逻辑函数的所有最小项用图形即小方格表示。B2023V1.1小方格在排列时,应使几何位置相邻的小方格,在逻辑上也是相邻的。所谓逻辑相邻,是指两个小方格所表示的最小项只有一个因子互为反变量即互补,而其余因子相同。按照这种相邻性原则排列的最小项方格图称为卡诺图。图6.8.1所示,分别是二、三、四变量的卡诺图。
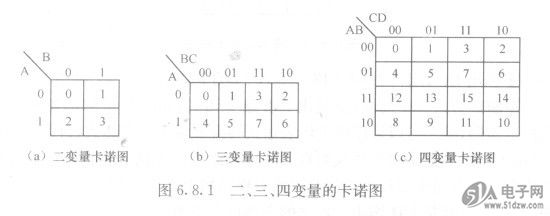
因为咒个变量的逻辑函数,有2”个最小项。因此,相对应的卡诺图应有2”个方格。所以,二、三、四变量卡诺图分别有4、8、16个方格,每个方格对应一个最小项。方格中的十进制数字是最小项的编号,也是卡诺图中方格的编号。在方格图外面标出了行与列各变量的取值。例如,三变量卡诺图中的1号方格,行变量A取值是0,列变量B、C取值是0、1,因此,1号方格对应变量A、B、C的取值是001,它对应的最小项是ABC又如,四变量卡诺图中的7号方格,对应变量A、B、C,D的取值是0111,它对应的最小项是ABCD。因此,卡诺图中方格及其编号与最小项是一一对应的。
(a)二变量卡诺图 (b)三变量卡诺图 (c)四变量卡诺图
图6.8.1二、三、四变量的卡诺图
在卡诺图中必须保证几何位置相邻的方格对应的最小项,具有逻辑相邻性。为此,卡诺图中行和列变量的取值必须按00、01、11、10的顺序排列。
需要注意的是,卡诺图中同一行的最左和最右方格,同一列的最上和最下方格也是逻辑相邻的,即具有循环邻接的特性。由此可知,4个角的方格也是逻辑相邻的。依照同样方法,可以画出五变量以上卡诺图。但因变量增多,卡诺图变得复杂,故应用较少。
为了便于化简,把逻辑函数的所有最小项用图形即小方格表示。B2023V1.1小方格在排列时,应使几何位置相邻的小方格,在逻辑上也是相邻的。所谓逻辑相邻,是指两个小方格所表示的最小项只有一个因子互为反变量即互补,而其余因子相同。按照这种相邻性原则排列的最小项方格图称为卡诺图。图6.8.1所示,分别是二、三、四变量的卡诺图。
因为咒个变量的逻辑函数,有2”个最小项。因此,相对应的卡诺图应有2”个方格。所以,二、三、四变量卡诺图分别有4、8、16个方格,每个方格对应一个最小项。方格中的十进制数字是最小项的编号,也是卡诺图中方格的编号。在方格图外面标出了行与列各变量的取值。例如,三变量卡诺图中的1号方格,行变量A取值是0,列变量B、C取值是0、1,因此,1号方格对应变量A、B、C的取值是001,它对应的最小项是ABC又如,四变量卡诺图中的7号方格,对应变量A、B、C,D的取值是0111,它对应的最小项是ABCD。因此,卡诺图中方格及其编号与最小项是一一对应的。
(a)二变量卡诺图 (b)三变量卡诺图 (c)四变量卡诺图
图6.8.1二、三、四变量的卡诺图

在卡诺图中必须保证几何位置相邻的方格对应的最小项,具有逻辑相邻性。为此,卡诺图中行和列变量的取值必须按00、01、11、10的顺序排列。
需要注意的是,卡诺图中同一行的最左和最右方格,同一列的最上和最下方格也是逻辑相邻的,即具有循环邻接的特性。由此可知,4个角的方格也是逻辑相邻的。依照同样方法,可以画出五变量以上卡诺图。但因变量增多,卡诺图变得复杂,故应用较少。
上一篇:逻辑函数的图形法化简
上一篇:逻辑函数的卡诺图化简


 公网安备44030402000607
公网安备44030402000607





